能用来做什么?
Kruskal重构树可以在线地求解带权无向图上,两点间所有路径中,权值最大(小)的边权值最小(大)的问题一看就很最小生成树
怎么做?
以最小生成树为例
普通的Kruskal求最小生成树,是在加边的过程中,利用冰碴鸡并查集检查是否会生成环,直接合并并查集并对边的端点u,v直接连边
而生成kruskal重构树,在加边过程中,则会进行如下操作:
建立一个新的点x,点权为边的权值,将u,v(或其所处树之树根)作为x的儿子
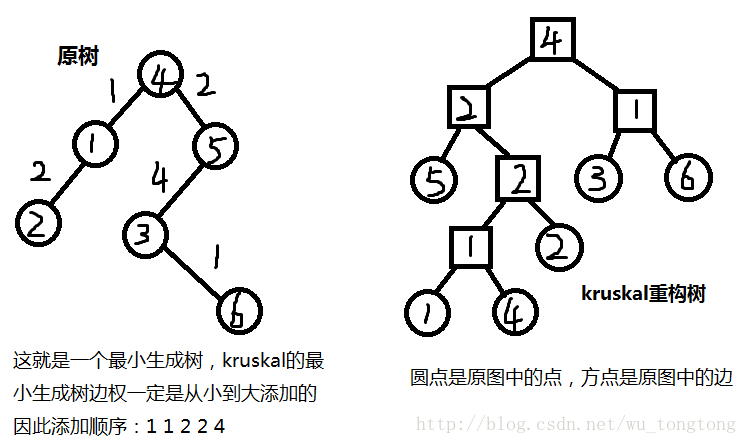
图源:https://blog.csdn.net/wu_tongtong/article/details/77601523
有什么性质?
这样生成的树有着十分优美的性质:
1:二叉树
2:最小生成树与重构树两点间路径上边权(点权)最大值相等
3:子节点点权小于父节点(大根堆)
4:最小生成树上两点间路径最大边权等于重构树上两节点的LCA之点权
真棒,有题吗?
bzoj3732 Network
Description
给你N个点的无向图 (1 <= N <= 15,000),记为:1…N。
图中有M条边 (1 <= M <= 30,000) ,第j条边的长度为: d_j ( 1 < = d_j < = 1,000,000,000).
现在有 K个询问 (1 < = K < = 20,000)。
每个询问的格式是:A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?
第一行: N, M, K。
第2…M+1行: 三个正整数:X, Y, and D (1 <= X <=N; 1 <= Y <= N). 表示X与Y之间有一条长度为D的边。
第M+2…M+K+1行: 每行两个整数A B,表示询问从A点走到B点的所有路径中,最长的边最小值是多少?
Output
对每个询问,输出最长的边最小值是多少。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
| 6 6 8
1 2 5
2 3 4
3 4 3
1 4 8
2 5 7
4 6 2
1 2
1 3
1 4
2 3
2 4
5 1
6 2
6 1
|
Sample Output
HINT
1
2
3
4
| 1 <= N <= 15,000
1 <= M <= 30,000
1 <= d_j <= 1,000,000,000
1 <= K <= 15,000
|
Solution
这就是裸题吧= =
直接用kruskal重构树秒之
Code
自己稍微YY了一下丑得一锤
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
| #include <cstdio>
#include <algorithm>
#include <cstring>
#include <cmath>
#include <iostream>
#include <queue>
#define maxn 15010
#define maxm 30010
using namespace std;
int n,m,k;
int prt[maxn*2][25],ch[maxn*2][2],uprt[maxn*2],dep[maxn*2];
long long pts[maxn*2];
struct edge
{
int u,v;
long long w;
}ing[maxm];
bool cmp(const edge &a,const edge &b)
{
return a.w<b.w;
}
int getroot(int x)
{
return uprt[x]==x?x:uprt[x]=getroot(uprt[x]);
}
void kruskal()
{
register int i;
int k=0;
for(i=1;i<=n*2;++i)
uprt[i]=i;
for(i=1;i<=m;++i)
{
int r1=getroot(ing[i].u),r2=getroot(ing[i].v);
if(r1!=r2)
{
++k;
uprt[r1]=uprt[r2]=prt[r1][0]=prt[r2][0]=n+k;
ch[n+k][0]=r1;
ch[n+k][1]=r2;
pts[n+k]=ing[i].w;
if(k==n-1)
return;
}
}
}
void dfs(int u,int depth)
{
dep[u]=depth;
register int i;
int v;
for(i=1;(1<<i)<=dep[u];++i)
{
prt[u][i]=prt[prt[u][i-1]][i-1];
}
if(ch[u][0])
dfs(ch[u][0],depth+1);
if(ch[u][1])
dfs(ch[u][1],depth+1);
}
int LCA(int x,int y)
{
if(dep[x]<dep[y])
swap(x,y);
register int i;
for(i=20;i>=0;--i)
if(dep[x]-(1<<i)>=dep[y])
x=prt[x][i];
for(i=20;i>=0;--i)
if(prt[x][i]!=prt[y][i])
{
x=prt[x][i];
y=prt[y][i];
}
x=prt[x][0];
return x;
}
int main()
{
scanf("%d%d%d",&n,&m,&k);
register int i;
int x,y;
for(i=1;i<=m;++i)
scanf("%d%d%lld",&ing[i].u,&ing[i].v,&ing[i].w);
sort(ing+1,ing+m+1,cmp);
kruskal();
dfs(2*n-1,1);
for(i=1;i<=k;++i)
{
scanf("%d%d",&x,&y);
printf("%lld\n",pts[LCA(x,y)]);
}
return 0;
}
|
另外,NOI2018 D1T1 归程,也要用到Kruskal重构树
BZOJ 3551 Peaks加强版 Kruskal重构树+主席树 已填坑
待AC。。。
题外话…
学习kruskal重构树过程中,这篇博客给了我很大的便利和启发,本文的一些内容也参考了这篇博客:
https://blog.csdn.net/oi_konnyaku/article/details/78757761
非常感谢博客作者的心血,为后来者铺平了道路

